• Individual catalog generation: SExtractor is run in double-image mode on the individual images
• Point source separation: For each pointing
• Catalog masking: Areas where photometric measurements and detections may be compromised are masked.
• Extinction: Extinction is computed for each object
• Catalog merging: The masked catalogs for each pointing are combined and redundant sources (ones which appear in more than one individual catalogs) are removed.
• Column definitions

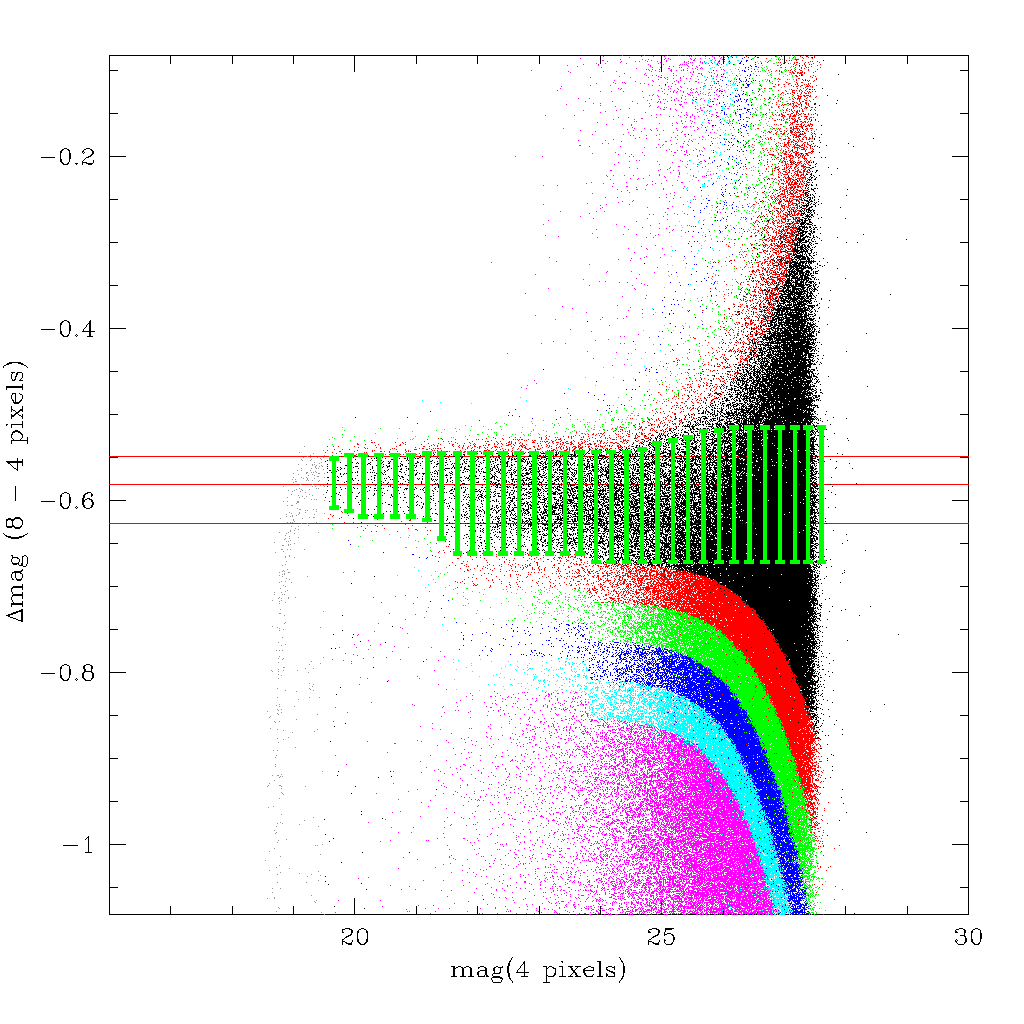
APS=(ΔMag-ΔMag_cen)/(sqrt(σ_Δ²+σMag²))

The combined width (σ_Δ and M_ERR added in quadrature) is indicated on the plot at right by the green error bars. So the APS nnumber is effectively a probability that the object is stellar, with small (absolute) numbers corresponding to high probabilities that the souce is point-like.

Note that, when calculating the width of the stellar locus, bin sizes of 0.25 mags are used (or a minimum of 50 objects if the bin would contain less than 50 objects). Further, the width is calculated independantly above and below the position of the locus. Finally, the algorithm imposes additional constraint that the locus can never get thinner with fainter magnitudes, and that the width of the locus can never be more than twice the width calculated at bright magnitudes (to stop it blowing up at faint magnitudes).

This technique appears to work well to within approximately 1 magnitude of the completeness limits (ie to 24th magnitude or so). Below this, galaxies start being misidentified as stars.

In general, any objects within 1.5 sigma of the stellar locus in both filters have a very high probability of being stellar (modulo the caveat at faint magnitudes). Ultimately, inspection of the diagnostic plots, and the science case that is actually being addressed, will drive the selection criteria. The plot at right shows objects with different values of APS indicated by different colours:

black	abs(APS)<1
red	1 <abs(APS)<1.5
green	1.5<abs(APS)<2
blue	2 <abs(APS)<2.5
cyan	2.5<abs(APS)<3
magenta	3 <abs(APS)

In addition, in some fields you can see a sequence running parallel to the stellar sequence below the stellar sequence. These are globular clusters in Virgo, which are usually slightly more resolved than a star, and hence lie just below the stellar sequence. The APS value (Alan's Point Sourciness, named after Alan McConnachie) is computed for the g and i bands.

E(B-V) can be converted into extinction in each band using the following table. The table gives the filter, reference wavelength of and coefficient A_λ/E(B-V) as determine with the York Extincion Solver using the Fitzpatrick (1999) extincion law.

Filter	Reference Wavelength	Coefficient
u	3747	4.594
g	4857	3.560
r	6272	2.464
i	7631	1.813
z	9635	1.221

One is to divide the NGVS fields with a grid corresponding the boundaries between pointings. Sources detected inside the boundary of a pointing are added to the catalog. Source outside the boundary are ignored since the will presumably be detected in the adjacent pointing. This is the "razor" method. The problem with this method is that if there is any uncertainty in the position of objects near a boundary it may double counted (position errors may shift it over the boundary into both adjacent pointings) or be missed entirely (position errors may shift it out of both pointings)

The other extreme is to include all objects from all the catalogs and then run a filter to determine which objects have been duplicated. Source which come from different catalogs but lie within some small radius of each other are probably the same source; one then eliminates the redundant source. This the "merge" method. The problem with this method is that the chance of two real different sources lying near each other may be non-negligible as shown in the figure below.

There are two parameters in this method: θ_overlap and θ_match. Changing either parameter significantly (doubling or halving it) had only a very small effect on the final merged catalogs: the total number of sources would change by a few hundred in a catalog of 24 million sources.

Boundaries were also applied at the edges of the main NGVS field and the four background fields. The boundaries lie at the point where the effective exposure time of the images (as indicated by weight map) drops to half of the nominal value. A list of all the pointing boundaries can be found here.